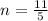Question

Find the value of m and n so that tha function . = + −x a solution of Given differential equations ′′ − ′ − = 0 () = , ′() = 2

Answer 1

Question:

Determine the value of m and n so that the following system of linear equation have an infinite number of solutions.

`(2m-1)x+3y-5=0`

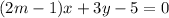
and

`3x+(n-1)y-2=0`

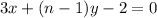
Answer:

`m=(17)/(4)`

`n = (11)/(5)`

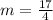
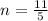
Explanation:

Given

`3x+(n-1)y-2=0`

`(2m-1)x+3y-5=0`

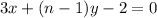
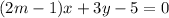
Rewrite both equations:

`3x + (n - 1)y = 2`

`(2m - 1)x + 3y = 5`

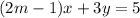
For the expression to have a solution, the following condition must exist:

`(3x)/((2m - 1)x) = ((n-1)y)/(3y)= (2)/(5)`

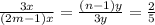
Split to 2

`(3x)/((2m - 1)x) = (2)/(5)`

`((n-1)y)/(3y)= (2)/(5)`

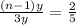
Cross Multiply

`5 * 3x = 2 * (2m - 1)x` -- (1)

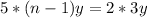`5 * (n -1)y = 2 * 3y` -- (2)

Solving (1)

`5 * 3x = 2 * (2m - 1)x`

Divide both sides by x

`5 * 3 = 2 * (2m - 1)`

Open bracket

`15 = 4m - 2`

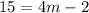
Collect Like Terms

`4m = 15+2`

`4m= 17`

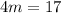
Make m the subject

`m=(17)/(4)`

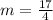
Solving (2)

`5 * (n -1)y = 2 * 3y`

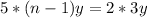
Divide both sides by 7

`5 * (n - 1) = 2 * 3`

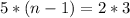
Open bracket

`5n - 5 = 6`

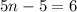
Collect Like Terms

`5n = 5 + 6`

`5n = 11`

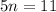
Make n the subject

`n = (11)/(5)`