Question

There is no smallest positive rational number because, if there were, then it could be divided by two to get a smaller one. EXPLAINED

Answer 1

Since a/2⁽ⁿ ⁺ ¹⁾b < a/2ⁿb, we cannot find a smallest positive rational number because there would always be a number smaller than that number if it were divided by half.

Explanation:

Let a/b be the rational number in its simplest form. If we divide a/b by 2, we get another rational number a/2b. a/2b < a/b. If we divide a/2b we have a/2b ÷ 2 = a/4b = a/2²b. So, for a given rational number a/b divided by 2, n times, we have our new number c = a/2ⁿb where n ≥ 1

Since
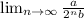`\lim_(n \to \infty) (a)/(2^(n)b )` = a/(2^∞)b = a/b × 1/∞ = a/b × 0 = 0, the sequence converges.

Now for each successive division by 2, a/2⁽ⁿ ⁺ ¹⁾b < a/2ⁿb and

a/2⁽ⁿ ⁺ ¹⁾b/a/2ⁿb = 1/2, so the next number is always half the previous number.

So, we cannot find a smallest positive rational number because there would always be a number smaller than that number if it were divided by half.