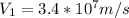Answer:
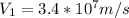
Step-by-step explanation:
From the question we are told that
Nucleus diameter
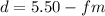
a 12C nucleus
Required kinetic energy
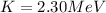
Generally initial speed of proton must be determined,applying the law of conservation of energy we have
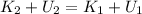
where
 =initial kinetic energy
=initial kinetic energy
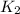 =final kinetic energy
=final kinetic energy
 =initial electric potential
=initial electric potential
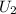 =final electric potential
=final electric potential
mathematically
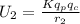
where
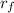 =distance b/w charges
=distance b/w charges
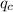 =nucleus charge
=nucleus charge
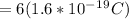
 =constant
=constant
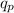 =proton charge
=proton charge
Generally kinetic energy is know as
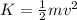
Therefore
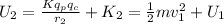
Generally equation for radius is
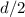
Mathematically solving for radius of nucleus
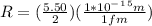
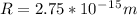
Generally we can easily solving mathematically substitute into v_1
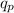
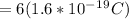
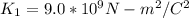
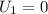
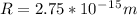
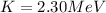

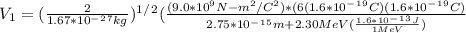
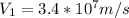
Therefore the proton must be fired out with a speed of