Question

Unpolarized light with intensity 300 W/m^2 passes first through a polarizing filter with its axis vertical, then through a second polarizing filter. It emerges from the second filter with intensity 121 W/m^2. What is the angle from vertical of the axis of the second polarizing filter?

Answer 1

The angle from vertical of the axis of the second polarizing filter is 50.57⁰.

Step-by-step explanation:

Given;

intensity of the unpolarized light, I₀ = 300 W/m²

intensity of emergent polarized light, I = 121 W/m²

let the angle from vertical of the axis of the second polarizing filter = θ

Apply Malus's law, intensity of emergent polarized light is given as;

I = I₀Cos²θ

`Cos^2 \theta = (I)/(I_o) \\\\Cos^2 \theta =(121)/(300) \\\\Cos^2 \theta =0.4033\\\\Cos \theta = √(0.4033) \\\\Cos \theta = 0.6351\\\\\theta = Cos^(-1) (0.6351)\\\\\theta = 50.57 ^0`

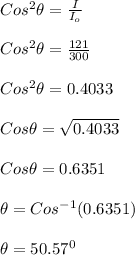
Therefore, the angle from vertical of the axis of the second polarizing filter is 50.57⁰.