Question

A cyclist is coasting at 13 m/s when she starts down a 460 m long slope that is 30 m high. The cyclist and her bicycle have a combined mass of 70 kg. A steady 15 N drag force due to air resistance acts on her as she coasts all the way to the bottom. What is her speed at the bottom of the slope?

Answer 1

The value is
`v = 23.6 \ m/s`

Step-by-step explanation:

From the question we are told that

The velocity is
`u = 13 \ m/s`

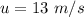
The length of the slope is
`l = 460 \ m`

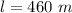
The height of the slope is
`h = 30 \ m`

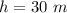
The mass of the cyclist and her bicycle is
`m = 70 \ kg`

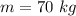
The drag force is
`F = 15 \ N`

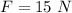
Generally from the law of energy conservation we have that

`PE + KE_t = W * KE_b`

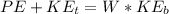
Here
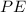`PE` is the potential energy at the top of the slope which is mathematically represented as

`PE = m* g * h`

=>
`PE = 70 * 9.8 * 30`

=>
`PE = 20580 \ J`

and
`KE_t` is the kinetic energy at the top of the slope which is mathematically represented as

`KE_t = (1)/(2) * m * u^2`

=>
`KE_t = (1)/(2) * 70 * 13^2`

=>
`KE_t = 5915 \ J`

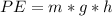
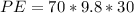
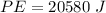
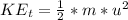
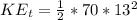
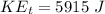
And W is the work done by the bicycle which is mathematically represented as

`W = F * l`

=>
`W = 15 * 460`

=>
`W = 6900 \ J`

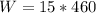
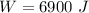
and
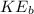`KE_b` is the kinetic energy at the bottom of the slope which is mathematically represented as

`KE_b = (1)/(2) * m * v^2`

=>
`KE_b = (1)/(2) * 70 * v^2`

=>
`KE_b = 35 v^2`

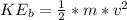
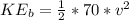
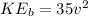
So

`20580 + 5915 = 6900 + 35 v^2`

=>
`v = 23.6 \ m/s`