Question

An ideal gas resides in a closed cylinder (diameter is 0.5 ft) with a frictionless piston. The initial conditions are 139 mol of the ideal gas at 25°C. The piston is compressed isothermally to one third of the initial volume. The heat capacity C_v of an ideal gas is 1.5 middot R.

Required:
a. What is the heat interaction (kJ) for this process?
b. The piston now expands isothermally to 120% of the same initial volume. Will the heat interaction increase, decrease, or stay the same?

Answer 1

a. 3.79e5 J

b. Decrease.

Step-by-step explanation:

Hello!

a. In this case, since the heat involved during a compression-expansion isothermal process is computed via:

`Q=nRTln((V_2)/(V_1) )`

Now, since the final volume is one third of the initial one:

`V_2=(V_1)/(3)`

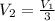
So we can plug in now:

`Q=139mol*8.3145(J)/(mol*K)*298.15K*ln(((V_1)/(3) )/(V_1) )\\\\Q=-3.79x10^5J`

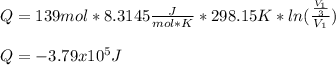
b. In this case, the relationship between initial and final volume is:

`V_2=2.2V_1`

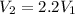
So the heat interaction is now:

`Q=139mol*8.3145(J)/(mol*K)*298.15K*ln((2.2V_1 )/(V_1) )\\\\Q=2.72x10^5J`

It means that the heat interaction decrease on the contrary process, it means that in a. heat was released by 3.79e5 J and in b heat is absorbed by 2.72e5 J.

Best regards!