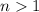Question

a sequence has a first number of 3 and a half common difference of 4 what is the recursive rule of nth term​

Answer 1

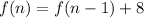`f(n) = f(n-1) + 8` for
`n > 1`

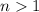
Explanation:

Given

`f(1) = 3` -- First Term

`(1)/(2)d = 4` --- half common difference

Required

Find the recursive rule

First, we calculate the common difference

`(1)/(2)d = 4`

Multiply through by 2

`2 * (1)/(2)d = 2 * 4`

`d = 8`

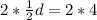
The second term of the sequence is:

`f(2) = 3 + 8 = 11`

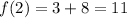
The third term is:

`f(3) = 11 + 8 = 20`

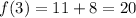
So, we have:

`f(1) = 3`

`f(2) = 3 + 8`

Substitute f(1) for 3

`f(2) = f(1) + 8`

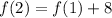
Express 1 as 2 - 1

`f(2) = f(2-1) + 8`

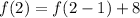
Substitute n for 2

`f(n) = f(n-1) + 8`

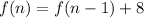
Similarly:

`f(3) = 11 + 8`

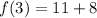
Substitute f(2) for 11

`f(3) = f(2) + 8`

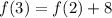
Express 2 as 3 - 1

`f(3) = f(3-1) + 8`

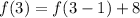
Substitute n for 3

`f(n) = f(n-1) + 8`

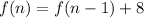
Hence, the recursive is:

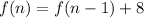`f(n) = f(n-1) + 8` for
`n > 1`