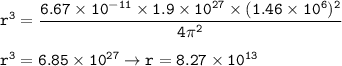Question

Callisto is a moon of Jupiter (mass = 1.90 x 1027 kg), which orbits the planet with a period of 16.9 days. What is the radius of its orbit?​

Answer 1

The radius of its orbit = 8.27 x 10¹³ m

Further explanation

Given

mass Jupiter=1.9 x 10²⁷ kg

T = 16.9 days=1.46 x 10⁶ s

Required

the radius =r

Solution

To hold the moon in its orbit, the gravitational force between two objects (jupiter and moon) will be equal to the centripetal force

`\tt G(M.m)/(r^2)=m.(v^2)/(r)\rightarrow v=(2.\pi.r)/(T)\\\\M=(r^3.4\pi^2)/(T^2.G)\rightarrow r^3=(GMT^2)/(4\pi^2)`

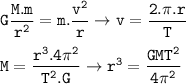
G = 6.67 x 10⁻¹¹ N/m²kg²

Input the value :

`\tt r^3=(6.67* 10^(-11)* 1.9* 10^(27)* (1.46* 10^6)^2)/(4\pi^2)\\\\r^3=6.85* 10^(27)\rightarrow r=8.27* 10^(13)`