Question

A beach ball is inflated so its diameter increases from 12 inches to 12.5 inches. Given that the formula for the volume of a sphere is V=4/3π,r^3 the change in the volume of the beach ball using differentials is approximately.

a. 367π cubic inches.
b. 727π cubic inches.
c. 1447π cubic inches.
d. 288.7π cubic inches.

Answer 1

V = 36π cubic inches.

Explanation:

Given that:

The volume of the sphere is
`V = (4)/(3) \pi r^3`

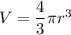
If the diameter is represented by P.

Then P = 2r

and r = P/2

∴

`V = (4)/(3) \pi ( (P)/(2))^3`

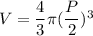
By differentiating both sides;

`dV = (4)/(3) \pi * 3 ( (P)/(2))^2 * (1)/(2) * dP`

`dV = (1)/(2) \pi P^2 \ dP`

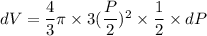
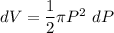
where;

P = 12

dP = 12.5 - 12

dP = 0.5

Then;

`(1)/(2) \pi ( 12)^2 * 0.5`

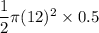
= 36π

Thus, the volume is V = 36π cubic inches.