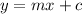Question

What is the equation of the graphed line written in

standard form?
Ox-4y = 4
Ox+4y = 4
(4,0)
Oy-x-1
Oy-1
45
o,-1)

Answer 1

the third option is the answer, y= 1/4x-1

Explanation:

graph line in standard form:

`y = mx + c`

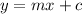
where m = slope and c = y-intercept

1) find the slope

slope formula:

`(y2 - y1)/(x2 - x1)`

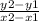
use the two coordinates given in the graph

i/ (0,-1)

x1 = 0

y1 = -1

ii/ (4,0)

x2 = 4

y2 = 0

substitute the values into the formula

`(y2 - y1)/(x2 - x1)`

`(0 - ( - 1))/(4 - 0)`

`(1)/(4)`

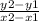
thus, m = 1/4

2) find the y-intercept

* y-intercept is the value of y that cuts through the y-axis

based on the graph, the y-intercept is -1

thus, c = -1

3) substitute the value of m and c into the standard form formula

`y = mx + c`

`y = (1)/(4) x - 1`