Question

Find the value of sin(a/2) if cosa= 12/13
​

Answer 1

Answer: sin
`(a)/(2)` = ±
`(1)/(√(26) )`

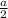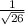
Explanation:

We very well know that,

cos2A=1−2sin²A

⟹ sinA = ±
`√((1-) (cos2A)/(2) )`

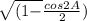
As required, set A =
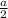`(a)/(2)` & cos a=
`(12)/(13)` ,thus we get

sin
`(a)/(2)` =±
`\sqrt{(1-cos a)/(2) }`

∴ sin
`(a)/(2)` =±
`\sqrt{(1-(12)/(13) )/(2) }` = ±
`(1)/(√(26) )`

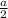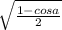
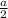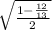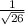
since ,360° <
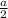`(a)/(2)` <450°

,180° <
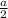`(a)/(2)` <225°

Now, we are to select the value with the correct sign. It's is obvious from the above constraints that the angle a/2 lies in the III-quadrant where 'sine' has negative value, thus the required value is negative.

hope it helped!