Answer:
Half life = 4.7 days
Explanation:
Formula to get the final amount of the substance after the time 't',
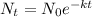
Here,
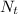 = Final amount of the substance
= Final amount of the substance
 = Initial amount
= Initial amount
k = decay constant
t = Duration or time
Now by substituting the values in the formula,
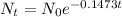
If
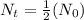 [For half life]
[For half life]
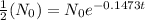
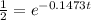
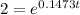
ln(2) =
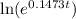
0.69315 = 0.1473t
t = 4.71 days
t ≈ 4.7 days
Therefore, half life of the substance is 4.7 days.