Question

What is the factored form of ...

Answer 1

The answer is A:

`(x^(4)y^(6) - 1)(x^(8)y^(12) - x^(4)y^(6) + 1)`

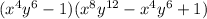
Explanation:

To solve this question, first apply the exponent rule to the entire equation:

`x^(12)y^(18) + 1`

`= (x^(4)y^(6))^(3) + 1^(3)`

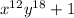
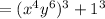
Next, we can apply the Sum of Cubes formula. To refresh your memory, the formula is as thus:

`x^(3) + y^(3) = (x + y)(x^(2) - xy + y^(2))`

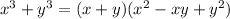
So, let's apply this to the equation above:

`(x^(4)y^(6))^(3) + 1^(3)`

`= (x^(4)y^(6) + 1)((x^(4)y^(6))^(2) - x^(4)y^(6) + 1^(2))`

`= (x^(4)y^(6) + 1)((x^(4)y^(6))^(2) - x^(4)y^(6) + 1^(2))`

`= (x^(4)y^(6) - 1)(x^(8)y^(12) - x^(4)y^(6) + 1)`

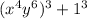
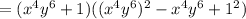
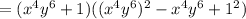
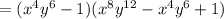
Therefore, the answer is A.

Hope this helped!

Answer 2

(A) I think

Explanation:

We you divide x12 and y18,12=4 y=6. Then you take +1 and change it to -1. It should bring you to answer A.

I hope I'm right and I hope this helps:)!