Question

B. Find the standard deviation of the data.

c. Explain what the mean and standard deviation tell you about the data you
collected
HELPPPPPP

Answer 1

b. The standard deviation for class 1 is approximately 18.81415

The standard deviation for class 2 is approximately 16.1527

The standard deviation for class 3 is approximately 12.705

c. The mean of the data indicates that the average scores of Class 1 and Class 2 are equal and less than the average score of Class 3

The standard deviation indicates that the data in Class 1 varies more than the data in Class 2, and also, that the data of Class 2 varies more than the data of Class 3.

Explanation:

b. The mean and the standard deviation can be calculated using Microsoft Excel with the values presented here as results as follows;

The standard deviation, σ is given by the formula
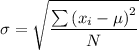`\sigma =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)}`, while the formula mean, μ is
`\mu = (\Sigma x)/(N)`

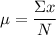
Where;

N = The number of terms = 12

∑x = 946 for Class 1, 953 for Class 2, 953 for Class 3

The mean for Class 1 = ∑x for Class 1/N = 946/12 = 78.8
`\bar 3`

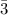
The mean for Class 2 = ∑x for Class 2/N = 953/12 = 79.41
`\bar 6`

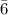
The mean for Class 3 = ∑x for Class 3/N = 953/12 = 79.41
`\bar 6`

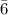
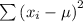`\sum \left (x_i-\mu \right )^(2) }` for Class 1 = 4247.
`\bar 6`

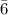
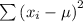`\sum \left (x_i-\mu \right )^(2) }`/N = for Class 1 = 353.97
`\bar 2`

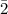
The standard deviation for class 1 σ₁, is given as follows;

`\sigma_1 =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)} = √(353.97\bar 2 ) \approx 18.81415`

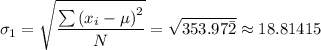
The standard deviation for class 1 = 18.81415

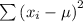`\sum \left (x_i-\mu \right )^(2) }` for Class 2 = 3130.9167

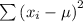`\sum \left (x_i-\mu \right )^(2) }`/N = for Class 2 = 260.90972

The standard deviation for class 2 σ₂, is given as follows;

`\sigma_2 =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)} \approx √(260.90972 ) \approx 16.1527`

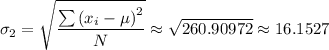
The standard deviation for class 2 = 16.1527

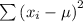`\sum \left (x_i-\mu \right )^(2) }` for Class 3 ≈ 1936.917

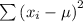`\sum \left (x_i-\mu \right )^(2) }`/N = for Class 3 ≈ 161.4097222

The standard deviation for class 3 σ₃, is given as follows;

`\sigma_3 =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)} \approx √(161.40972 ) \approx 12.705`

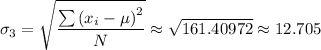
The standard deviation for class 3 ≈ 12.705

c. The mean indicates that the average score for Class 1 is higher than the average score for Class 2, and that the average score for Class 2 is the same as the average score for Class 3

However, the standard deviation indicates that the variability of the scores for Class 1 is higher than the variability of the scores for Class 2, and that there is also a higher variability in the scores of Class 2 than the variability in the scores of class 3