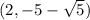1 Answer

Synapse · Answer 1 · 2023-12-18T00:52:17+0000

Explanation:

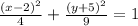
$\frac{(x - 2) {}^(2) }{4} + \frac{(y + 5) {}^(2) }{9} = 1$

This is the equation of the ellipse. Since the denominator is greater for the y values, we have a vertical ellipse. Remember a>b, so a

The formula for the foci of the vertical ellipse is

(h,k+c) and (h,k-c).

where c is

Our center (h,k) is (2, -5)

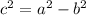
${c}^(2) = {a}^(2) - {b}^(2)$

Here a^2 is 9, b^2 is 4.

${c}^(2) = 9 - 4$

${c}^(2) = 5$

c = √(5)

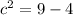
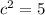
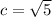
So our foci is

(2, - 5 + √(5) )

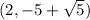
and

(2, - 5 - √(5) )

Please log in or register to add a comment.