Answer:
Steps include:
- Find the ratio between the mass of this hypothetical planet and the mass of planet earth.
- Calculate the ratio between the acceleration of free fall (gravitational field strength) near the surface of that hypothetical planet and near the surface of the earth.
Assumption: both planet earth and this hypothetical planet are spheres of uniform density.
Step-by-step explanation:
Mass of that hypothetical planet
Let
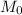 ,
,
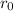 , and
, and
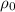 denote the mass, radius, and density of planet earth.
denote the mass, radius, and density of planet earth.
The radius and density of this hypothetical planet would be
 and
and
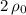 , respectively.
, respectively.
The volume of a sphere is
 .
.
Therefore:
- The volume of planet earth would be
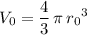 .
.
- The volume of this hypothetical planet would be:
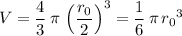 .
.
The mass of an object is the product of its volume and density. Hence, the mass of the earth could also be represented as:
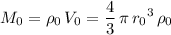 .
.
In comparison, the mass of this hypothetical planet would be:
 .
.
Compare these two expressions. Notice that
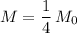 . In other words, the mass of the hypothetical planet is one-fourth the mass of planet earth.
. In other words, the mass of the hypothetical planet is one-fourth the mass of planet earth.
Gravitational field strength near the surface of that hypothetical planet
The acceleration of free fall near the surface of a planet is equal to the gravitational field strength at that very position.
Consider a sphere of uniform density. Let the mass and radius of that sphere be
 and
and
 , respectively. Let
, respectively. Let
 denote the constant of universal gravitation. Right next to the surface of that sphere, the strength of the gravitational field of that sphere would be:
denote the constant of universal gravitation. Right next to the surface of that sphere, the strength of the gravitational field of that sphere would be:
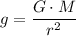 .
.
(That's the same as if all the mass of that sphere were concentrated at a point at the center of that sphere.)
Assume that both planet earth and this hypothetical planet are spheres of uniform density.
Using this equation, the gravitational field strength near the surface the earth would be:
 .
.
.
On the other hand, the gravitational field strength near the surface of that hypothetical planet would be:
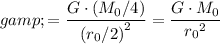 .
.
Notice that these two expressions are equal. Therefore, the gravitational field strength (and hence the acceleration of free fall) would be the same near the surface of the earth and near the surface of that hypothetical planet.
As a side note, both
 and
and
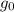 could be expressed in terms of
could be expressed in terms of
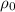 and
and
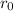 alongside the constants
alongside the constants
 and
and
 :
:
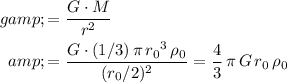 .
.
 .
.