Answer:
1) aser 1 has the maximum closest to the center
2) Δy = 0.0866 m , 3) Δy = 0.693 m
Step-by-step explanation:
The interference phenomenon is described by the expression
d sin θ = m λ for constructive interference
d sin θ = (m + ½) λ for destructive interference
We can use trigonometry to find the angle
tan θ = y / L
in trigonometry experiments the angles are small
tam θ =
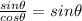
sin θ = y / L
we substitute
d y / L = m λ (1)
1) Let's find the first maximum that corresponds to m = 1 for each laser
laser 1 λ = d / 20
d y₁ / L = 1 d / 20
y₁ = L / 20
y₁ = 5.20 / 20
y₁ = 0.26 m
Laser 2 λ= d / 15
d y₂ / L = 1 d / 15
y₂ = d / 15
y₂ = 5.20 / 15
y₂ = 0.346 m
Therefore laser 1 has the maximum closest to the center
2) the difference between these maxima
Δy = y₂ - y₁
Δy = 0.3466 - 0.26
Δy = 0.0866 m
3) we look for the second maximum m = 2 of laser 1, we substitute in equation 1
y₃ = 2 5.20 / 20
y₃ = 0.52 m
now let's find the third minimum m = 3 of laser 2
d y₄ / L = (m + ½) λ
d y₄ / 5.20 = (3 + ½) d / 15
y₄ = 3.5 5.20 / 15
y₄ = 1.213 m
Δy = y₄ -y₃
Δy = 1.213 - 0.52
Δy = 0.693 m