Question

Dan is driving from his hometown to California to Colorado for a ski vacation. The equation defines the distance he is from home h hours after noon. What are the meanings of the values in the equation?

y=70h+100
a. Dan is 100 miles from home at noon and is traveling at 70 miles per hour.
b. Dan is 70 miles from home at noon and is traveling at 100 miles per hour.
c. Dan leaves at 1:00 and is traveling at 70 miles per hour.
d. Dan leaves at noon and is traveling at 100 miles per hour.

Answer 1

A is the right answer.

Explanation:

Answer 2

a. Dan is 100 miles from home at noon and is travelling at 70 miles per hour.

Explanation:

Given

`y = 70h + 100`

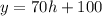
Required

Interpret

An equation has the form

`y = mx + b`

Where

`m = rate`

`b = y\ intercept`

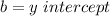
By comparison with
`y = 70h + 100`

`m = 70`

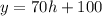
i.e. He travels at 70 miles per hour

And

`b = 100`

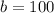
This represents the initial distance as at when he started travelling (12 noon)

i.e. At noon, he is 100 miles away from home