Question

Quickly plz What is the value of x?

O liv units
O 2 13 units
O 2/3 units
O 3v3 units

Answer 1

`x=3√(2)\\`

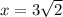
Explanation:

Since the smaller triangles have a side of the same length, they share one side, and the included angle is 90°, the triangles are congruent.

This means the length of the side to the left is also x as shown in the image below.

The bigger triangle is also right and has side lengths of x, x, and 6 (the hypotenuse), thus:

`x^2+x^2=6^2`

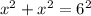
Operating:

`2x^2=36`

`x^2=18`

Since 18=9*2

`x=√(9*2)`

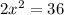
`\mathbf{x=3√(2)}`

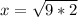
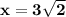
The options are not clear enough, so I cannot make a choice.