Question

Are the equations 2x - y = - 4 and 3x + y = -1 dependent, independent or neither

Answer 1

From the above calculations, it is clear that the consistent system has exactly one solution i.e. x = -1, y =2, therefore, it is independent.

Explanation:

Given the system of equations

`\begin{bmatrix}2x-y=-4\\ 3x+y=-1\end{bmatrix}`

`\mathrm{Multiply\:}2x-y=-4\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:6x-3y=-12`

`\mathrm{Multiply\:}3x+y=-1\mathrm{\:by\:}2\:\mathrm{:}\:\quad \:6x+2y=-2`

`\begin{bmatrix}6x-3y=-12\\ 6x+2y=-2\end{bmatrix}`

`6x+2y=-2`

`-`

`\underline{6x-3y=-12}`

`5y=10`

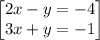
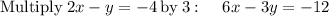
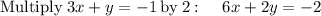
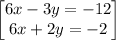
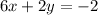
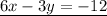
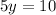
so the system of equations becomes

`\begin{bmatrix}6x-3y=-12\\ 5y=10\end{bmatrix}`

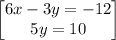
solving 5y = 10 for y

`5y=10`

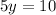
Divide both sides by 5

`(5y)/(5)=(10)/(5)`

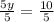
simplify

`y=2`

`\mathrm{For\:}6x-3y=-12\mathrm{\:plug\:in\:}y=2`

`6x-3\cdot \:2=-12`

`6x-6=-12`

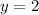
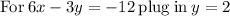
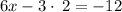
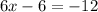
Adding 6 to both sides

`6x-6+6=-12+6`

`6x=-6`

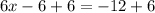
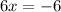
Divide both sides by 6

`(6x)/(6)=(-6)/(6)`

`x=-1`

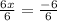
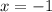
Therefore, the solution to the system of equations be:

`x=-1,\:y=2`

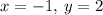
From the above calculations, it is clear that the consistent system has exactly one solution i.e. x = -1, y =2, therefore, it is independent.