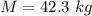Question

A meter stick is found to balance at the 49.7-cm mark when placed on a fulcrum. When a 41.5-gram mass is attached at the 28.5-cm mark, the fulcrum must be moved to the 39.2-cm mark for balance. What is the mass of the meter stick

Answer 1

The value is
`M = 42.3 \ kg`

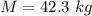
Step-by-step explanation:

From the question we are told that

The first position of the fulcrum is x = 49.7 cm

The mass attached is
`m = 41.5 \ g`

The position of the attachment is
`x_1 = 28.5 \ cm`

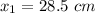
The second position of the fulcrum is
`x_2 = 39.2 \ cm`

Generally the sum of clockwise torque = sum of anti - clockwise torque

So

`CWT = m (x_2 - x_1)`

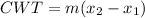
Here CWT stands for clockwise torque

`ACWT = M ( x - x_2)`

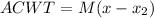
So

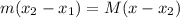
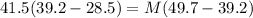
`m (x_2 - x_1) = M ( x - x_2)`

=>
`41.5 (39.2 - 28.5 ) = M ( 49.7 -39.2 )`

=>
`M = 42.3 \ kg`