Question

Which system of equations is satisfied by the solution shown on the graph?

Answer 1

Answer: D x + y = 6 and x − y = -10

Explanation:

Answer 2

D

Explanation:

To find the system of equations that is satisfied by the solution shown on the graph, we will simply need to find the equations of our two lines.

So, we will begin by finding the slope of each line and then proceed to find the entire equation.

Red Line:

To find the slope, we will first pick any two points from the red line.

Two sample points include (-5, 5) and (-4, 6).

The slope formula is given by:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

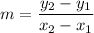
Lett (-5, 5) be (x₁, y₁) and (-4, 6) be (x₂, y₂). Substitute:

`\displaystyle m=(6-5)/(-4-(-5))=(1)/(1)=1`

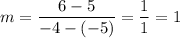
Hence, the slope of the red line is 1.

Now, we can find the entire equation. We will use the slope-intercept form:

`y=mx+b`

Where m is the slope and b is the y-intercept.

We know that the slope m is 1. Hence:

`y=x+b`

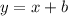
We need to find our y-intercept b. For the red line, we know that when x is -5, y is 5. Hence:

`(5)=(-5)+b`

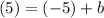
Solving for b yields:

`b=10`

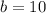
Therefore, our entire equation is:

`y=x+10`

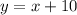
Blue Line:

Again, we will find the slope first.

Picking two points, we get (0, 6) and (1, 5).

Using the slope formula by letting (0, 6) be (x₁, y₁) and (1, 5) be (x₂, y₂), we acquire:

`\displaystyle m=(5-6)/(1-0)=(-1)/(1)=-1`

Hence, the slope of the blue line is -1.

Again, we can use the slope-intercept form:

`y=mx+b`

Fortunately, we already know the y-intercept in this case. Since we have the point (0, 6), the y-intercept b is 6.

Therefore, our equation is:

`y=-x+6`

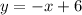
So, our two equations are:

`y=x+10\text{ and } y=-x+6`

Our answers are in standard form, so we will convert the two equations to standard form. Standard form is given by:

`Ax+By=C`

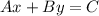
Where A, B, and C are integers and A is positive.

For the first equation, we can subtract x from both sides to get:

`-x+y=10`

Since A should be positive, we multiply both sides to get:

`x-y=-10`

For the second equation, we can add x to both sides:

`x+y=6`

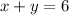
Hence, our two equations in standard form is:

`x+y=6\text{ and } x-y=-10`

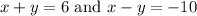
Therefore, our final answer is D.