Answer:
a}
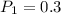
b)
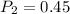
c) NOT INDEPENDENT
Explanation:
From the question we are told that
Sample space
Math majors are 3
computer science majors are 3
Generally the sample space is
Mathematically the sample space required on Monday is given as
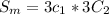
where
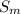 =sample space on Monday
=sample space on Monday
Therefore,
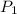 =
=
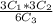
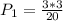
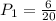
b)
Generally the the equation is given as
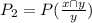
where
x is selecting two math major and 1 computer science major on Monday
y is at leas one math major selected
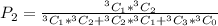
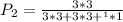
c)
Generally in representing independent events

=>

Mathematically
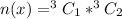

therefore

This does not satisfy the two equations stated above therefore NOT INDEPENDENT