Question

A block of ice has a square top and bottom and rectangular sides. At a certain point in

time, the square top and bottom each have a length of 30 cm, which are decreasing at a
rate of 2 cm/h. At the same time, the height of the ice block is 20 cm and decreasing at
3 cm/h. How fast is the ice melting?

Answer 1

`(dV)/(dt) = 360 \ cm^3/h`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

Geometry

• Volume of a Rectangular Prism: V = lwh

Calculus

Derivatives

Derivative Notation

Differentiating with respect to time

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

`l = 30 \ cm\\w = l\\(dl)/(dt) = 2 \ cm/h\\h = 20 \ cm\\(dh)/(dt) = 3 \ cm/h`

Step 2: Differentiate

1. Rewrite [VRP]:
   `V = l^2h`
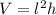
2. Differentiate [Basic Power Rule]:
   `(dV)/(dt) = 2l(dl)/(dt) (dh)/(dt)`

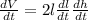
Step 3: Solve for Rate

1. Substitute:
   `(dV)/(dt) = 2(30 \ cm)(2 \ cm/h)(3 \ cm/h)`
2. Multiply:
   `(dV)/(dt) = 360 \ cm^3/h`

Here this tells us that our volume is decreasing (ice melting) at a rate of 360 cm³ per hour.