Question

The graph represents function 1, and the equation represents function 2:

6
3
2
1
0
0 1
2
3
4
5 6 7 8 9
Function 2
y = 8x + 12
How much more is the rate of change of function 2 than the rate of change of function 1? (4 points)
O 3
O4
O 5

Answer 1

Please check the explanation.

Explanation:

We know that the slope or rate of change of the function can be:

• positive

• negative

• zero, or

• undefined

Function 1

From the function 1 graph, it is clear that the graph is a horizontal line. We must note that the horizontal line has a slope or rate of change zero. The reason is that the horizontal line can not rise vertically. i.e. y₂-y₁=0

so using the slope formula

Rate of change = m = y₂-y₁ / x₂-x₁

Taking two points (x₁, y₁) = (0, 4), (x₂, x₁) = (1, 4)

Rate of change = m = 4-4 / 1-0

Rate of change = m = 0/1

Rate of change = m = 0

Thus, the rate of change of function 1 is zero.

Function 2

We know the slope-intercept form of linear equation is

`y = mx+b`

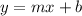
where m is the rate of change or slope of the function and b is the y-intercept

Given the function

`y = 8x+12`

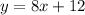
comparing with the slope-intercept form i.e. y = mx+b

Therefore, the rate of change of function 2 = m = 8

Conclusion

The rate of change of function 1 = 0

The rate of change of function 2 = 8

as

• 8 - 0 = 8

Therefore, function 2 has 8 more rate of change of function than the rate of change of function 1.