Answer:
The smallest composite number for
 is 24, which is the product 2 and 12.
is 24, which is the product 2 and 12.
Explanation:
A composite number is an integer that is not a prime number, that is, a number that can be divided only by one and itself. Let be
 the smallest composite number such that there are two positive integers
the smallest composite number such that there are two positive integers
 ,
,
 such that
such that
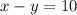 and
and
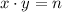 .
.
 is a positive integer, since both integers are positive. Then, we can use the following formula:
is a positive integer, since both integers are positive. Then, we can use the following formula:
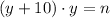

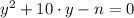 (1)
(1)
We obtain the roots of this second order polynomial by means of the Quadratic Formula:
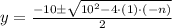
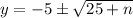 (2)
(2)
Given that
 , we must observe the following inequation:
, we must observe the following inequation:
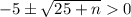 (3)
(3)

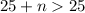
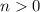
Let is find the values of x and y by iterative means:
x = 11, y = 1
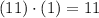
11 is not a composite number, but a prime number.
x = 12, y = 2
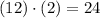
24 is a composite number, which contains the following product of prime numbers:
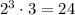
The smallest composite number for
 is 24, which is the product 2 and 12.
is 24, which is the product 2 and 12.