Question

A car weighing 19600N is moving with a speed of 30 m/sec on a level road. If it is brought to rest in a distance of 100 m. Find the average distance friction force acting on it

Answer 1

F = -8820 N

Step-by-step explanation:

Given that,

The weight of a car, W = 19600 N

Initial speed of the car, u = 30 m/s

It is brought to rest, final velocity, v = 0

Distance, d = 100 m

We need to find the average friction force acting on it.

Firstly we find the acceleration of the car using third equation of motion. Let it is a.

`v^2-u^2=2as\\\\a=(v^2-u^2)/(2d)\\\\a=((0)^2-(30)^2)/(2* 100)\\\\=-4.5\ m/s^2`

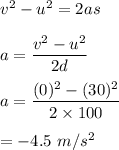
Average frictional force,

F = ma

m is mass,
`m=(W)/(g)=(19600\ N)/(10\ m/s^2)=1960\ kg`

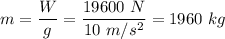
F = 1960 kg × -4.5 m/s²

= -8820 N

So, the average friction force acting on it is 8820 N.