Question

An astronaut floating at rest in space throws a wrench in one direction and subsequently recoils back with a velocity in the opposite direction. Which of the following statements is/are true?

I. The velocity of the wrench is equal and opposite to the velocity of the astronaut.
Il. The momentum of the wrench is equal and opposite to the momentum of the astronaut.
III. The impulse applied to the wrench is equal and opposite to the impulse applied to the astronaut
a) ll and ill only
b) I only II only
c) I, II, and III
d) I and Il only

Answer 1

a) ll and Ill only

Step-by-step explanation:

Let the mass of the wrench = m

and the mass of the astronaut = M

Initially, the velocity of the astronaut and wrench are zero.

The astronaut throws the wrench in one direction and subsequently recoils back with a velocity in the opposite direction.

Let v and V be the velocity of the wrench and the velocity of the astronaut respectively.

In space, there is no external force acting, the momentum must be conserved.

So, m(0)+M(0)=m(v)+M(V)

So, 0=mv+MV

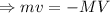`\Rightarrow mv=-MV` ...(i)

Here, the momentum of the wrench = mv, and the momentum of the astronaut= MV. The negative sign showing that both the momentum are in opposite direction.

Therefore, the momentum of the wrench is equal and opposite to the momentum of the astronaut.

According to Newton's second law, the rate of change of momentum = applied force.

Let it take
`\Delta t` seconds to change the momentum.

So, for the wrench

`m(v-0)/\Delta t= F_w \\\\\Rightarrow m(v-0)=F_w\Delta t \\\\\Rightarrow mv=F_w\Delta t \cdots(ii)`

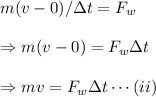
Here,
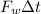`F_w\Delta t` is the impulse applied to the wrench.

Similarly, for the astronaut

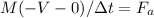`M(-V-0)/\Delta t= F_a` [negative sign (-V) for opposite direction]

`\Rightarrow M(-V-0)=F_a\Delta t \\\\\Rightarrow -MV=F_a\Delta t`

Here,
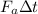`F_a\Delta t` is the impulse applied to the astronaut.

So, the impulse on the astronaut.

By using equations (i) and (ii)

`F_a\Delta t=F_w\Delta t`

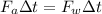
Therefore, the impulse applied to the wrench is equal and opposite to the impulse applied to the astronaut.

Hence, option (a) is correct.