Answer:
(a) 26.83 m
(b) 12.65 m/s
(c) 3.2 seconds
(d) 3.2 seconds
(e) 38.4 m
(f) 12.8 m
Step-by-step explanation:
Given that a projectile launched at a speed of 20m/s above the horizontal axis at an angle of 53 degrees.
The vertical component of the velocity in the upward direction,
u= 20 sin 53= 20 x 0.8 = 16 m/s.
The horizontal component of the initial velocity,
s=20 cos53 = 20x0.6=12 m/s.
As the gravitational force acts in the vertical direction, so it will only change the vertical component of the initial velocity while the horizontal component of the initial velocity remains unchanged.
(a) The displacement at 2 seconds:
The horizontal distance covered in 2 seconds = 12x2= 24 m
By using the equation of motion, s= ut +1/2 at²
Here, a= -10 m/s² (as g=10m/s² acts in the downward direction)
the vertical displacement s= 16x2- 1/2 x 10 x 2²=12 m
Hence, the displacement after 2 seconds =
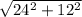 =26.83 m
=26.83 m
(b) The velocity at 2 seconds:
As the horizontal component of the velocity is not changing, so the horizontal component of the velocity = 12 m/s
By using the equation of motion, v=u+at
The vertical component of the velocity, v= 16 - 10x2=-4m/s
The negative sign shows that the vertical component of the velocity is in the downward direction.
So, the the velocity at 2 seconds = 12 i - 4 j m/s
The magnitude of the velocity =
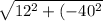 =12.65 m/s
=12.65 m/s
(c) Total time of flight:
Total time of flight = 2 x (time to reach the maximum height)
At maximum height, the vertical component of the velocity = 0
So, by using the equation of motion, v=u+at
0= 16-10 t
t= 16/10=1.6 seconds
Hence, the total time of flight= 2 x 1.6 = 3.2 seconds.
(d) Maximum time:
This is the same as the total time of flight, so the maximum time = 3.2 seconds.
(e) Range:
Range = Horizontal component of the velocity x total time of flight
= 12 x 3.2 = 38.4 m
(f) Maximum height:
As the time to reach the highest point = 1.6 seconds
So, by using the equation of motion s = ut + 1/2 at²
The maximum height, s = 16 x 1.6 + 1/2 (-10)1.6² =12.8 m
Hence, the maximum height is 12.8 m.