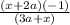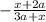Answer:
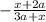
Step-by-step explanation:
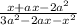
i) write ax as a difference
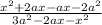
ii) write -2ax as a difference
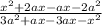
iii) factor out x from the expression
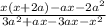
iv) factor out -a from the expression
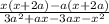
v) factor out a from the expression
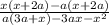
vi) factor out -x from the expression
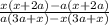
vii) factor out x+2a from the expression
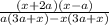
viii) factor out 3a+x from the expression
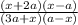
ix) factor out the negative sign from the expression and rearrange the term
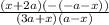
x) reduce the fraction a-x