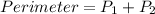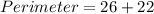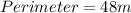Answer:
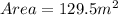
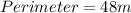
Explanation:
Given
See attachment
Required
Determine the area and the perimeter of the garden
Calculating Area
First, we calculate the

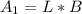
Where:
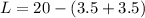
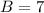
So:

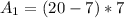
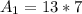
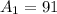
Next, we calculate the area of the two semi-circles.
Two semi-circles = One Circle
So:
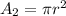
Where
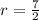
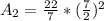
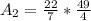
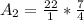

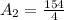
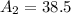
Area of the garden is
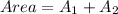
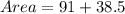
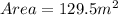
Calculating Perimeter
First, we calculate the perimeter of the rectangle
But in this case, we only consider the length because the widths have been covered by the semicircles
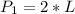
Where:
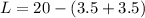
So:
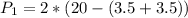

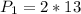

Next, we calculate the perimeter of the two semi-circles.
Two semi-circles = One Circle
So:
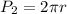
Where
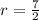

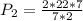
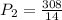
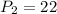
Perimeter of the garden is