Question

A 0.9 kg ball attached to a cord is whirled in a vertical circle of radius 2.5 m. Find the minimum speed needed at the top of the circle so that the cord remains taut and the ball’s path remains circular.

Answer 1

The minimum speed needed at the top of the circle so that the cord remains tensioned and the ball's path remains circular is approximately is 9.903 meters per second.

Step-by-step explanation:

By the Principle of Energy Conservation we understand that the minimum speed needed by the ball is that speed such that maximum height reached is equal to the diameter of the vertical circle, that is:

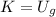`K =U_(g)` (1)

Where:

`K` - Translational kinetic energy, measured in joules.

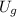`U_(g)` - Gravitational potential energy, measured in joules.

By definitions of translational kinetic and gravitational potential energies, we expand the equation above and clear the initial speed of the ball:

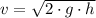`(1)/(2)\cdot m \cdot v^(2) = m\cdot g\cdot h`

`v = √(2\cdot g\cdot h)` (2)

Where:

`m` - Mass, measured in kilograms.

`v` - Initial speed, measured in meters per second.

`g` - Gravitational acceleration, measured in meters per square second.

`h` - Maximum height of the ball, measured in meters.

If we know that
`g = 9.807\,(m)/(s^(2))` and
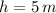`h = 5\,m`, then the initial speed of the ball is:

`v = \sqrt{2\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (5\,m)}`

`v\approx 9.903\,(m)/(s)`

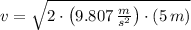
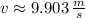
The minimum speed needed at the top of the circle so that the cord remains tensioned and the ball's path remains circular is approximately is 9.903 meters per second.