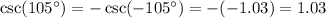Answer:
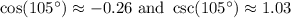
Explanation:
We are given that:

And we want to find:

Part A)
Remember that cosine (and secant) is an even function. By definition, this means that:
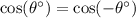
Therefore, since we know that cos(-105°) is about -0.26, it follows from the definition that:
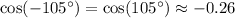
Part B)
Remember that cosecant (and sine) is an odd function. By definition, this means that:
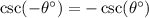
We know that csc(-105°) is about -1.03.
By the above definition, we can rewrite csc(105°) as csc(-(-105°)) or -csc(-105°).
Hence, it follows that: