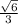Answer:
sin θ =
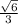
Explanation:
Given that,
cos θ =
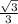
From the trigonometric functions,
cos θ =
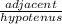
⇒ adjacent =
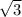 , and the hypotenuse = 3
, and the hypotenuse = 3
Let the opposite side be represented by x, applying the Pythagoras theorem we have;
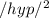 =
=
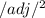 +
+
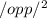
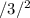 =
=
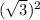 +
+
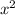
9 = 3 +
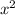
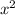 = 9 - 3
= 9 - 3
= 6
x =
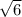
Thus, opposite side =
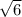
So that,
sin θ =
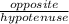
=
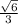
Therefore,
sin θ =