Question

A ray moving in water at 55.5 deg

enters plastic, where it bends to
48.7 deg. What is the index of
refraction for the plastic?
( water n = 1.33, Air n = 1.00 )

Answer 1

Refractive index of the plastic = 1.46

Step-by-step explanation:

By Snell's law,

`\frac{\text{sin}\theta _(2) }{\text{sin}\theta _(1)}=(n_1)/(n_2)`

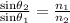
Here,
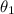`\theta _1` = Angle of incidence in medium 1 (Plastic)

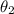`\theta_2` = Angle of refraction in medium 2 (Water)

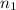`n_1` = Refractive index of medium 1 (Plastic)

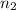`n_2` = Refractive index of medium 2 (Water)

By substituting values in the formula,

`\frac{\text{sin}(48.7)}{\text{sin}(55.5)}=(1.33)/(n_2)`

`n_2=\frac{1.33* \text{sin}(55.5)}{\text{sin}(48.7)}`

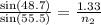
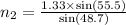
= 1.46

Therefore, refractive index of the plastic = 1.46