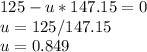Question

1. A 15 kg chair initially at rest on a horizontal floor requires 125 N to set it in motion, Ong

the chair is in motion, a 95 kg force keeps it moving at constant veloclty,
a Find the coefficient of static friction between the chair and the floor,

Answer 1

μ = 0.849

Step-by-step explanation:

In order to solve this problem we must remember that the friction force is defined as the product of the coefficient of friction by the normal force. And normal force is defined as the component of force in the opposite direction to the weight of the body (chair).

As in the y axis there is no movement we can say that the sum of the forces on the chair is equal to zero.

∑Fy = 0

`N-W=0`

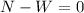
where:

N = normal force [N] (units of Newtons)

W = weight of the chair = m*g [N]

m = mass = 15 [kg]

g = gravity acceleration = 9.81 [m/s²]

`N=m*g\\N=15*9.81\\N=147.15 [N]`

Now the key to solving this problem is to understand that we start applying force on the horizontal component until the chair starts to move at this moment the friction component is calculated with the static friction coefficient. As the chair doesn't move we can say that the sum of force in the horizontal direction is equal to zero.

∑Fx = 0

`F -f_(force) = 0`

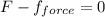
F = force applied = 125 [N]

fforce = friction force = μ*N

μ = friction coefficient (static)

N = normal force = 147.15 [N]

`125-u*147.15=0\\u = 125/147.15\\u = 0.849`