Answer:
y’ = 2x
Explanation:
Let y = f (x), take the natural logarithm of both sides ln (y) = ln (f (x))
ln (y) = ln (x²)
Differentiate the expression using the chain rule, keeping in mind that y is a function of x.
Differentiate the left hand side ln (y) using the chain rule.
y’/y = 2 In (x)
Differentiate the right hand side.
Differentiate 2 ln (x)
y’/y = d/dx = [ 2 In (x) ]
Since 2 is constant with respect to xx, the derivative of 2 ln (x) with respect to x is 2 d/dx [ln (x)]
y’/y = 2 d/dx [In (x)]
The derivative of ln (x) with respect to x is 1/x.
y’/y = 2 1/x
Combine 2 and 1/x
y’/y = 2/x
Isolate y' and substitute the original function for y in the right hand side.
y’ =
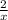 x²
x²
Factor x out of x².
y’ =
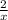 (x * x)
(x * x)
Cancel the common factor.
y’ =
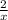 (x * x) (The x that is under 2 and the other x that I have underlined are the ones that cancel out)
(x * x) (The x that is under 2 and the other x that I have underlined are the ones that cancel out)
Rewrite the expression.
y’ = 2x
So therefore, the answer would be 2x.