Given:
Vertices of a parallelogram ABCD are A(7,-4), B(-1,-4), C(-1,-12), D(7, -12).
To find:
Whether the parallelogram ABCD is a rhombus, rectangle or square.
Solution:
Distance formula:

Using distance formula, we get
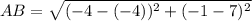
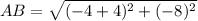
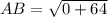
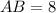
Similarly,
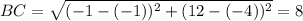
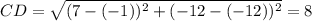
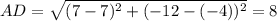
All sides of parallelogram are equal.
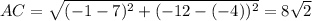
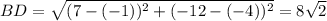
Both diagonals are equal.
Since, all sides are equal and both diagonals are equal, therefore, the parallelogram ABCD is a square.
We know that, a square is special case of rectangles and rhombus.
So, parallelogram ABCD is a rhombus, rectangle or square. Therefore, the correct option is c.