Question

Calculate the lenth of AC to 1 decimal place in the trapezium below.

Answer 1

18.1cm

Explanation:

Please refer to the attached photo for a better understanding. Apologies for the terrible drawing.

First we will find the length of BE by using pythagoras' Theorem.

`c^(2) =a^(2) +b^(2) \\AB^(2) =BE^(2) +EA^(2) \\16^(2) =BE^(2) +7^(2) \\256=BE^(2) +49\\BE^(2) =256-49\\BE=√(207) cm`

We will leave BE as it is as it is not the final answer.

Since we know CD = BE,

CD =
`√(207) cm`

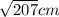
Now from the photo, draw a line from C to A or A to C, you will see another triangle.

Now we will use Pythagora's Theorem again to find AC.

`AC^(2) =AD^(2) +DC^(2) \\AC^(2) =11^(2) +(√(207)) ^(2) \\AC^(2) = 121+207\\AC^(2) =328\\AC=√(328) \\=18.1cm (1dp)`