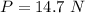Answer:
The value is
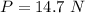
Step-by-step explanation:
From the question we are told that
The weight of the hollow cylinder is
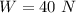
The radius of the hollow cylinder is
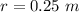
The distance which it is pulled is
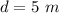
The velocity of the end of the rope is
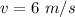
Gnerally the mass of the hollow cylinder is
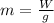
=>
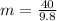
=>

Generally angular displacement for the distance covered is mathematically represented as

=>
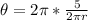
=>

=>
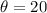
Generally the torque experienced by the hollow cylinder is mathematically represented as

Here I is the moment of inertia
=>

=>
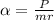
Generally from kinematic equation
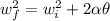
=>
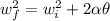
Generally the final angular velocity is mathematically
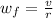
=>
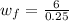
=>
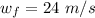
Generally the initial angular velocity is Zero given that the hollow cylinder was at rest before rolling
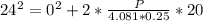
=>
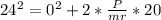
=>