Question

What is the domain of f?

Choose 1 answers
All real values of r such that=0
All real values of such that=0
All real values of such that r < 0
All real values of r such that >0
All real values of

Answer 1

Answer: C) All real values of x such that
`x \le 0`

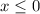
In other words, x must be 0 or smaller.

===================================================

Step-by-step explanation:

The reason why is because we must make the stuff under the square root to never be negative. We must make -2x be 0 or larger.

So,

`-2x \ge 0 \\\\-2x+2x \ge 0+2x \ \text{ ... add 2x to both sides}\\\\0 \ge 2x\\\\2x \le 0 \ \text{ ... flip both sides, and the inequality sign}\\\\x \le 0/2 \ \text{ ... divide both sides by 2}\\\\x \le 0`

As an example, if x = -2, then -2x = -2(-2) = 4 is positive. Applying the square root to a positive number is valid.

But if x = 5, then -2x = -2*5 = -10 is under the square root, which is not allowed.