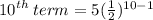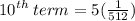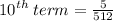Question

Someone please explain step by step.

Find the 10th term of the geometric sequence whose common ratio is 1/2
and whose first term is 5.
​

Answer 1

`{10}^(th) \: term = (5)/(512)`

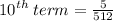
Explanation:

geometric progression formula:

`{n}^(th) \: term = ar ^(n - 1)`

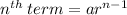
given:

common ratio, r = 1/2

`first \: term \: = 5`

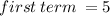
1) find the value of a

`{n}^(th) \: term \: = a {r}^(n - 1)`

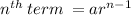
we're finding the 1st term, so substitute 1 into n:

`{1}^(st) \: term = a( (1)/(2) ) {}^(1 - 1)`

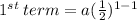
first term is 5. so we substitute 5 into the equation:

`5 = a(1)`

`a = 5`

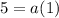
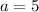
2) find the 10th term

we're finding the 10th term, so substitute 10 into the equation and don't forget to substitute 5 into a:

`{10}^(th) \: term = 5( (1)/(2) ) {}^(10 - 1)`

`{10}^(th) \: term = 5( (1)/(512) )`

`{10}^(th) \: term = (5)/(512)`