Answer:
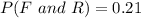
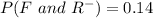
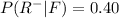



Explanation:
The variables have been defined in the question as:
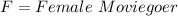
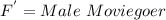
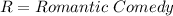
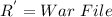
Also, we have the following given parameters:
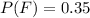

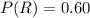
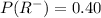
The solution is as follows:

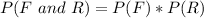
Substitute values for P(F) and P(R)
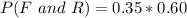
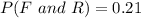
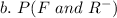
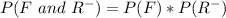
Substitute values for P(F) and P(R-)
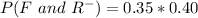
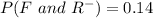

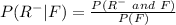
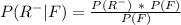
Substitute values for P(F) and P(R-)
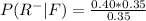
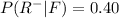
This implies that both events are independent
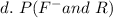
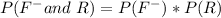
Substitute values for P(F-) and P(R)


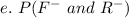
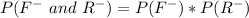
Substitute values for P(F-) and P(R-)
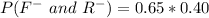

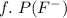
 --- Given
--- Given