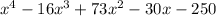Explanation:
Use this algebra 2 theorem:
If r and q are roots of a polynomial function then
the polynomial function can be expressed as
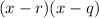
Here the roots are
1- root of 6, 1+ root 6, and. 7-i so our. function can be expressed as
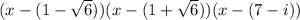
The first two binomials are difference off squares so the we have
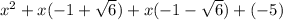
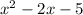
The other root is (7-i).
Also note since (7-i) is a root, then (7+I) is also a root.
So
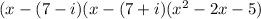
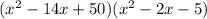
Simplify and it gives us