Question

A hose on the ground projects a water current upwards at an angle 40 to the horizontal at velocity 20 m/s find height at which water hits a wall at 8 m away from the hose (consider that acceleration due to gravity =9.8 m/s2)

Answer 1

The water hits the wall at a height of 5.38 m

Step-by-step explanation:

Projectile Motion

It's the type of motion that experiences an object projected near the Earth's surface and moves along a curved path exclusively under the action of gravity.

The object describes a parabolic path given by the equation:

`{\displaystyle y=\tan(\theta )\cdot x-{\frac {g}{2v_(0)^(2)\cos ^(2)\theta }}\cdot x^(2)}`

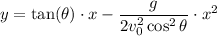
Where:

y = vertical displacement

x = horizontal displacement

θ = Elevation angle

vo = Initial speed

The hose projects a water current upwards at an angle of θ=40° at a speed vo=20 m/s.

The height at which the water hits a wall located at x=8 m from the hose is:

`{\displaystyle y=\tan40^\circ\cdot 8-{\frac {9.8}{2*20^(2)\cos ^(2)40^\circ }}\cdot 8^(2)}`

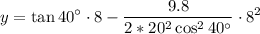
Calculating:

y = 5.38 m

The water hits the wall at a height of 5.38 m