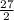Question

Determine the

the fourth
the geometric sequence. x; 2x+2; 3x+3.
numerical
value
Of
term
OF​

Answer 1

a₄ = -
`(27)/(2)`

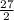
Explanation:

In a geometric sequence, the common ratio r is calculated as

r =
`(a_(2) )/(a_(1) )` =
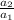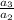`(a_(3) )/(a_(2) )` , substitute values

`(2x+2)/(x)` =
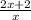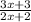`(3x+3)/(2x+2)` ( cross- multiply )

(2x + 2)² = x(3x + 3) ← expand both sides

4x² + 8x + 4 = 3x² + 3x ( subtract 3x² + 3x from both sides )

x² + 5x + 4 = 0 ← in standard form

(x + 1)(x + 4) = 0 ← in factored form

Equate each factor to zero and solve for x

x + 1 = 0 ⇒ x = - 1

x + 4 = 0 ⇒ x = - 4

However x ≠ - 1 as this would make the denominator of the second term equal to zero and therefore undefined.

Thus x = - 4 and

r =
`(2(-4)+2)/(-4)` =
`(-8+2)/(-4)` =
`(-6)/(-4)` =
`(3)/(2)`

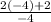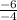Then

a₁ = - 4

a₂ = - 4 ×
`(3)/(2)` = - 6

a₃ = - 6 ×
`(3)/(2)` = - 9

a₄ = - 9 ×
`(3)/(2)` = -
`(27)/(2)`