Options:
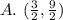

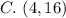
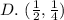
Answer:
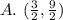
Explanation:
Given
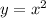
Required
Determine which of the given points is not true
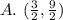
Here
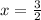 and
and
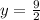
Substitute these values in
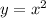
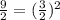

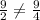
Both sides of the equation are not equal. Hence, this point do not line on the curve

Here
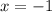 and
and
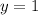
Substitute these values in
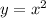
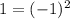

Both sides of the equation are equal. Hence, this point line on the curve
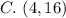
Here
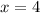 and
and
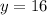
Substitute these values in
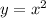

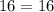
Both sides of the equation are equal. Hence, this point line on the curve
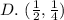
Here
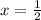 and
and
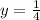
Substitute these values in
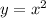
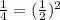
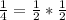

Both sides of the equation are equal. Hence, this point line on the curve
From the calculations above; only
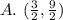 do no lie on the curve
do no lie on the curve