Question

a body attains its maximum height at H . it covers 3H÷4 height at time T . then how much time will it take to cover remaining H÷4​

Answer 1

The time it takes the body to cover the remaining H/4 is T

Step-by-step explanation:

The maximum height attained by the body = H

The time it takes the body to reach 3/4×H = T

From the kinematic equation, h = u·t - 1/2·g·t², we have;

u = 0 m/s at for the object returning back down at maximum height, therefore at the maximum height, we have;

H = u × 0 + 1/2·g·t²

H = 1/2·g·t²

t = √(2·H/g)

When h = 3/4×(H) from below, we have;

h = H/4 from above, which gives;

`t_(H/4)` = √(2·H/4/g) = √(H/(2·g)) = 1/2 × √(2·H/g)

∴ The time it takes the body to cover H/4 height, while falling from above
`t_(H/4)` = 1/2 × √(2·H/g)

The time,
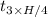`t_(3 * H/4)`, it takes to cover the remaining 3/4×(H) while falling from above is
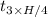`t_(3 * H/4)` = T = t - 1/2 × √(2·H/g) = √(2·H/g) - 1/2 × √(2·H/g) = 1/2 × √(2·H/g)

∴ T = 1/2 × √(2·H/g)

Therefore, the time it takes the body to reach a height of 3/4H = The time it takes the body to cover the remaining H/4 = T.