Question

Amplitude of 16 units, a period of 5 units, a vertical displacement of 3 units up and a phase shift of 2.5 units left.

Answer 1

The question is incomplete. The complete question is :

A sine function that has an amplitude of 16 units, a period of 5 units,a vertical displacement of 3 units up and a phase shift of 2.5 units left. Graph this function and show each step.

Solution :

The standard form of the sine function is

y = a sin (bx - c) + d

Here given :

Amplitude, a = 16

Period :
`$(2 \pi)/(|b|) = 5$`

⇒
`$b = (2\pi)/(5)$`

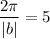
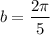
Phase shift :
`$(c)/(b) = 2.5$`

`$\Rightarrow (c)/(2 \pi/5)=(5)/(2)$`

∴
`$c = - \pi$`

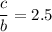
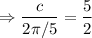
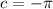
The vertical displacement : d = 3 units up

Now substituting a, b, c and d values in the standard form gives :

`$y = 16 \sin \left( (2 \pi)/(5)x -(- \pi)\right) + 3$`

`$y = 16 \sin \left( (2 \pi)/(5)x + \pi\right) + 3$`

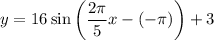
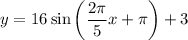
The graph is attached below.