Question

In isosceles triangle ABC the segment BD with D a point on AC is the median to the base AC. Find BD if the perimeter of ABC is 50m and the perimeter of ABD is 40m

Answer 1

Given:

In isosceles triangle ABC, consider AB=BC and the segment BD with D a point on AC is the median to the base AC.

Perimeter of ABC is 50m and the perimeter of ABD is 40m.

To find:

The length of BD.

Solution:

In isosceles triangle ABC the segment BD with D a point on AC is the median to the base AC.

`AB=BC` ...(i)

`AD=CD`

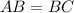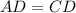
`AC=2AD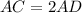` ...(ii)

Perimeter of ABC is 50m.

`AB+BC+AC=50`

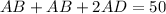`AB+AB+2AD=50` [Using (i) and (ii)]

`2AB+2AD=50`

`2(AB+AD)=50`

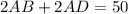
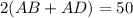
Divide both sides by 2.

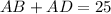`AB+AD=25` ...(iii)

Now, perimeter of ABD is 40m.

`AB+AD+BD=40`

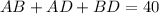
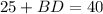`25+BD=40` [Using (iii)]

`BD=40-25`

`BD=15`

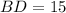
Therefore, the length of BD is 15m.